BELIEVE   ME   NOT!    - -     A   SKEPTIC's   GUIDE  

Galilean Transformations

So what? Well, this innocuous looking claim has some very perplexing logical consequences with regard to relative velocities, where we have expectations that follow, seemingly, from self-evident common sense. For instance, suppose the propagation velocity of ripples (water waves) in a calm lake is 0.5 m/s. If I am walking along a dock at 1 m/s and I toss a pebble in the lake, the guy sitting at anchor in a boat will see the ripples move by at 0.5 m/s but I will see them dropping back relative to me! That is, I can "outrun" the waves. In mathematical terms, if all the velocities are in the same direction (say, along x), we just add relative velocities: if v is the velocity of the wave relative to the water and u is my velocity relative to the water, then v', the velocity of the wave relative to me, is given by v' = v - u. This common sense equation is known as the GALILEAN VELOCITY TRANSFORMATION - a big name for a little idea, it would seem.

With a simple diagram, we can summarize the common-sense GALILEAN TRANSFORMATIONS (named after Galileo, no Biblical reference):

  

Figure: Reference frames of a "stationary" observer O and an observer O' moving in the x direction at a velocity u relative to O. The coordinates and time of an event at A measured by observer O are $\{x,y,z,t\}$ whereas the coordinates and time of the same event measured by O' are $\{x',y',z',t'\}$. An object at A moving at velocity $\Vec{v}_A$ relative to observer O will be moving at a different velocity $\Vec{v}_A'$ in the reference frame of O'. For convenience, we always assume that O and O' coincide initially, so that everyone agrees about the "origin:" when t=0 and t'=0, x=x', y=y' and z=z'.

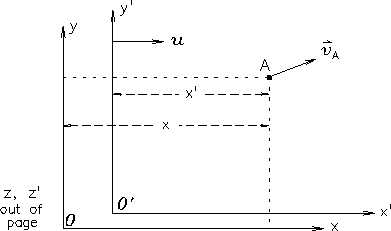First of all, it is self-evident that t'=t, otherwise nothing would make any sense at all.^23.1 Nevertheless, we include this explicitly. Similarly, if the relative motion of O' with respect to O is only in the x direction, then y'=y and z'=z, which were true at t=t'=0, must remain true at all later times. In fact, the only coordinates that differ between the two observers are x and x'. After a time t, the distance (x') from O' to some obect A is less than the distance (x) from O to A by an amount ut, because that is how much closer O' has moved to A in the interim. Mathematically, x' = x - ut.

The velocity $\Vec{v}_A$ of A in the reference frame of O also looks different when viewed from O' - namely, we have to subtract the relative velocity of O' with respect to O, which we have labelled $\Vec{u}$. In this case we picked $\Vec{u}$ along $\hat{x}$, so that the vector subtraction $\Vec{v}'_A = \Vec{v}_A - \Vec{u}$ becomes just v'_Ax = v_Ax - u while v'_Ay = v_Ay and v'_Az = v_Az. Let's summarize all these "coordinate transformations:"

    

This is all so simple and obvious that it is hard to focus one's attention on it. We take all these properties for granted - and therein lies the danger.