 - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE Suppose we have a point A in a plane with perpendicular x and y coordinate axes scribed on it, as pictured in Fig. 23.4.
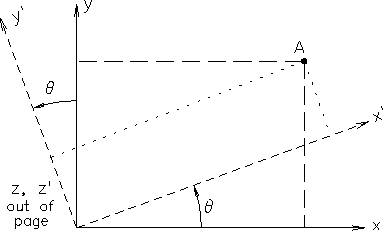 |
We can scribe a different pair of perpendicular coordinate
axes x' and y' on the same plane surface using dashed lines
by simply rotating the original coordinate axes by an angle
![]() about their common origin, the coordinates of which are
(0,0) in either coordinate system.
about their common origin, the coordinates of which are
(0,0) in either coordinate system.
Now suppose that we have the coordinates (xA,yA) of point A
in the original coordinate system and we would like to transform
these coordinates into the coordinates
(x'A,y'A) of the
same point in the new coordinate system.23.14
How do we do it? By trigonometry, of course. You can figure this out
for yourself. The transformation is
| x' | = | (23.2) | |
| y' | = | (23.3) |