BELIEVE ME NOT! -  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE


Next: Proper Time and Lorentz Invariants
Up: A Rotational Analogy
Previous: Rotation in Two Dimensions
If we now look at just the x and t part of the
LORENTZ TRANSFORMATION [leaving out the y and z parts,
which don't do much anyway], we have
| x' |
= |
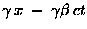 |
(23.4) |
| c t' |
= |
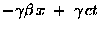 |
(23.5) |
-- i.e., the LORENTZ TRANSFORMATION "sort of" rotates
the space and time axes in much the same way as
a normal rotation of x and y. I have used ct as the
time axis to keep the units explicitly the same; if we use
"natural units" (c = 1) then we can just drop c out of
the equations completely and the analogy becomes obvious.
Jess H. Brewer -
Last modified: Mon Nov 23 11:05:17 PST 2015
 - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE