 - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE Picture a "snapshot" (holding time
Now let ![]() denote the displacement of particles of the medium
from their equilibrium positions. (I didn't use
denote the displacement of particles of the medium
from their equilibrium positions. (I didn't use ![]() here because
I am using that symbol for the area.
This may also differ between one end
of the cylindrical element and the other:
here because
I am using that symbol for the area.
This may also differ between one end
of the cylindrical element and the other:
![]() on the left vs.
on the left vs. ![]() on the right.
We assume the displacements to be in the
on the right.
We assume the displacements to be in the ![]() direction but very small compared to
direction but very small compared to ![]() , which is itself
no great shakes.14.10
, which is itself
no great shakes.14.10
The fractional change in volume ![]() of the cylinder
due to the difference between the displacements at the
two ends is
of the cylinder
due to the difference between the displacements at the
two ends is
Now, any elastic medium is by definition compressible but "fights back"
when compressed (![]() ) by exerting a pressure in the direction of
increasing volume. The BULK MODULUS
) by exerting a pressure in the direction of
increasing volume. The BULK MODULUS ![]() is a constant characterizing
how hard the medium fights back - a sort of 3-dimensional analogue
of the SPRING CONSTANT. It is defined by
is a constant characterizing
how hard the medium fights back - a sort of 3-dimensional analogue
of the SPRING CONSTANT. It is defined by
We now use
![]() on the mass element, giving
on the mass element, giving
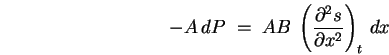
If we cancel ![]() out of Eq. (35), divide through by
out of Eq. (35), divide through by
![]() and collect terms, we get
and collect terms, we get
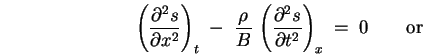
The fact that disturbances in an elastic medium obey the WAVE EQUATION
guarantees that such disturbances will propagate as
simple waves with phase velocity ![]() given by
Eq. (37).
given by
Eq. (37).
We have now progressed from the strictly one-dimensional propagation
of a wave in a taut string to the two-dimensional propagation of
waves on the surface of water to the three-dimensional propagation
of pressure waves in an elastic medium (i.e. sound waves);
yet we have continued to pretend that the only simple
type of traveling wave is a plane wave with constant ![]() .
This will never do; we will need to treat all sorts of wave phenomena,
and although in general we can treat most types of waves as
local approximations to plane waves (in the same way that we
treat the Earth's surface as a flat plane in most mechanics problems),
it is important to recognize the most important features of at least
one other common idealization - the SPHERICAL WAVE.
.
This will never do; we will need to treat all sorts of wave phenomena,
and although in general we can treat most types of waves as
local approximations to plane waves (in the same way that we
treat the Earth's surface as a flat plane in most mechanics problems),
it is important to recognize the most important features of at least
one other common idealization - the SPHERICAL WAVE.