BELIEVE   ME   NOT!    - -     A   SKEPTICs   GUIDE  

SOUND WAVES

Now let $s$ denote the displacement of particles of the medium from their equilibrium positions. This may also differ between one end of the cylindrical element and the other: $s$ on the left vs. $s+ds$ on the right. We assume the displacements to be in the $x$ direction but very small compared to $dx$, which is itself no great shakes.¹

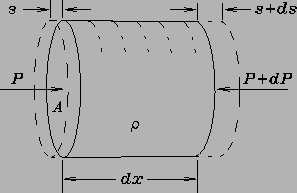
The fractional change in volume $dV/V$ of the cylinder due to the difference between the displacements at the two ends is

$${dV \over V} \; = \; {A(s+ds) - As \over Adx} \; = \; {ds . . . . . . r dx} \; = \; \left(\partial s \over \partial x \right)_t$$ (1)

where the rightmost expression reminds us explicitly that this description is being constructed around a "snapshot" with $t$ held fixed.

Now, any elastic medium is by definition compressible but "fights back" when compressed ($dV < 0$) by exerting a pressure in the direction of increasing volume. The BULK MODULUS $B$ is a constant characterizing how hard the medium fights back - a sort of 3-dimensional analogue of the spring constant. It is defined by

$$P \; = \; - B \, {dV \over V} .$$ (2)

Combining Eqs. (1) and (2) gives

$$P \; = \; - B \; \left(\partial s \over \partial x \right)_t$$ (3)

so that the difference in pressure between the two ends is

$$dP \; = \; \left(\partial P \over \partial x \right)_t \, d . . . . . . \; \left(\partial^2 s \over \partial x^2 \right)_t \, dx .$$ (4)

We now use $\sum F_x = m a_x$ on the mass element, giving

$$-A dP \; = \; A B \; \left(\partial^2 s \over \partial x^2 . . . . . . rho A dx \, \left(\partial^2 s \over \partial t^2 \right)_x$$ (5)

where we have noted that the acceleration of all the particles in the volume element (assuming $ds \ll s$) is just $a_x \equiv (\partial^2 s / \partial t^2 )_x$.

If we cancel $A dx$ out of Eq. (5), divide through by $B$ and collect terms, we get

$$\left(\partial^2 s \over \partial x^2 \right)_t \; - \; { . . . . . . \, \left(\partial^2 s \over \partial t^2 \right)_x \; = \; 0$$ (6)

which the acute reader will recognize as the WAVE EQUATION in one dimension ($x$), provided

$$c \; = \; \sqrt{B \over \rho}$$ (7)

is the velocity of propagation.

The fact that disturbances in an elastic medium obey the WAVE EQUATION guarantees that such disturbances will propagate as simple waves with phase velocity $c$ given by Eq. (7).