BELIEVE   ME   NOT!    -     A   SKEPTIC's   GUIDE  

Summary: The Exponential Function(s)

  

Figure: The functions  e^x, e^-x, 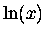$\ln(x)$ and 1/x  plotted on the same graph over the range from x=0 to x=4. Note that  $\ln(0)$  is undefined. [There is no finite power to which we can raise  e  and get zero.] Similarly,  1/x  is undefined at x=0, while   1/(-x) = - 1/x. Also,   $\ln(1) = 0$  [because any number raised to the zeroth power equals 1 - you can easily check this against the definitions] and  $\ln(\xi)$ [where $\xi$ any positive number less than 1] is negative. However, there is no such thing as the natural logarithm of any negative number.

Our formula (21) for the real value of your dollar as a function of time is the only function which will satisfy the differential equation (2) from which we started. The exponential function is one of the most useful of all for solving a wide variety of differential equations. For now, just remember this:

Whenever you have   ${dy \over dx} = k \, y$,  you can be sure that   $y(x) = y_0 \, e^{kx}$  where  y₀  is the "initial value" of y [when x=0]. Note that  k  can be either positive or negative.

Finally, note the property of the second derivative:

$${d^2y \over dx^2} \; = \; k^2 \, y .$$ (26)

We will see another equation almost like this when we talk about SIMPLE HARMONIC MOTION.