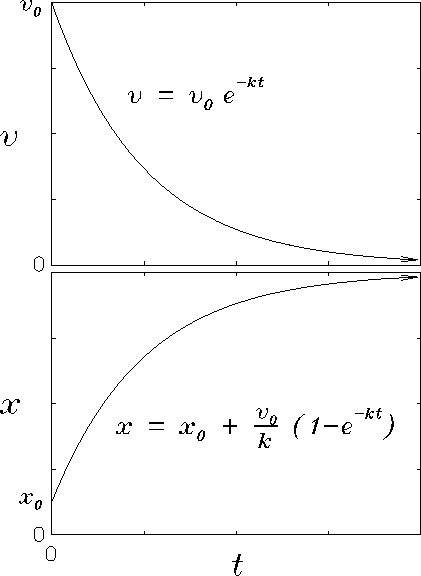Up: The Exponential Function
Previous: Summary: The Exponential Function(s)
We should really work out at least one example applying
the exponential function to a real Mechanics problem.
The classic example is where an object (mass m)
is moving with an initial velocity v0, starting
from an initial position x0, and experiences a
frictional damping force Fd which is
proportional to the velocity and (as always,
for frictional forces) in the direction opposite to the
velocity:
 .
The equation of motion then reads
.
The equation of motion then reads
 or
or
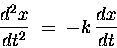 |
(27) |
where we have combined  and m into the
constant
and m into the
constant
 .
This can also be written in the form
.
This can also be written in the form
which should ring a bell!
The solution (for the velocity v) is
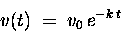 |
(28) |
To obtain the solution for x(t), we switch back to the notation
and note that the function whose time derivative is
 is
is
 ,
giving
,
giving
where the
![$[\cdots]_0^t$](img71.gif) notation means that the expression
in the square brackets is to be "evaluated between 0 and t"
-- i.e. plug in the upper limit (just t itself) for t
in the expression and then subtract the value of the
expression with the lower limit (0) substituted for t.
In this case the lower limit gives
e-0 = e0 = 1
(anything to the zeroth power gives one) so the result is
notation means that the expression
in the square brackets is to be "evaluated between 0 and t"
-- i.e. plug in the upper limit (just t itself) for t
in the expression and then subtract the value of the
expression with the lower limit (0) substituted for t.
In this case the lower limit gives
e-0 = e0 = 1
(anything to the zeroth power gives one) so the result is
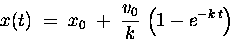 |
(29) |
The qualitative behaviour is plotted in Fig. 2.
Note that x(t) approaches a fixed "asymptotic" value
 as
as
 .
The generic function
.
The generic function
 is another useful addition
to your pattern-recognition repertoire.
is another useful addition
to your pattern-recognition repertoire.
Figure:
Solution to the damping force equation of motion,
in which the frictional force is proportional to the velocity.
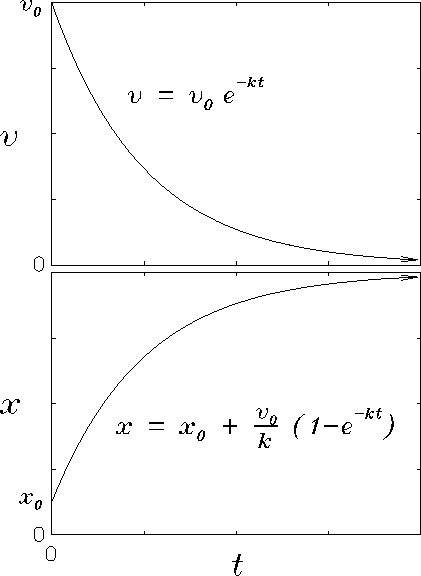 |



Up: The Exponential Function
Previous: Summary: The Exponential Function(s)
Jess H. Brewer -
Last modified: Fri Nov 13 17:22:01 PST 2015
![]() .
The equation of motion then reads
.
The equation of motion then reads
![]() or
or