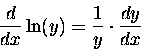BELIEVE ME NOT! -  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE


Next: Thermal Equilibrium
Up: Criterion for Equilibrium
Previous: Criterion for Equilibrium
Is there any way to derive a formal (mathematical) criterion
for the condition of thermal equilibrium, starting
from a hypothetical knowledge of 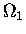 as a function of U1
and
as a function of U1
and 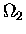 as a function of
U2 = U - U1?
Of course! Why else would I be doing this?
The thing about a maximum of a function
(or a minimum, for that matter; either type of extremum
obeys the same rule) is that the slope of the function
must be zero at the extremum.
[Otherwise it would still have further up or down to go!]
Since the slope is given by the derivative, this reads
as a function of
U2 = U - U1?
Of course! Why else would I be doing this?
The thing about a maximum of a function
(or a minimum, for that matter; either type of extremum
obeys the same rule) is that the slope of the function
must be zero at the extremum.
[Otherwise it would still have further up or down to go!]
Since the slope is given by the derivative, this reads
 |
(15.6) |
In this case, since
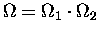 ,
the PRODUCT RULE for derivatives gives
,
the PRODUCT RULE for derivatives gives
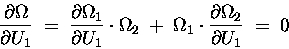 |
(15.7) |
Now, 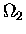 is a function of U2, not U1;
but we can get around that by using the CHAIN RULE,
is a function of U2, not U1;
but we can get around that by using the CHAIN RULE,
where
U2 = U - U1 and U is a constant, so
We can therefore substitute
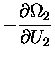 for
for
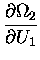 in Eq. (7):
in Eq. (7):
or
If we now divide both sides by the product
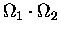 ,
we get
,
we get
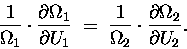 |
(15.8) |
Now we need to recall the property of the natural logarithm
that was so endearing when we first encountered it:
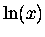 is the function whose derivative is the inverse,
is the function whose derivative is the inverse,
and, by the CHAIN RULE,
In this case "y" is 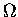 and "x" is U,
so we have
and "x" is U,
so we have
which means that Eq. (8) can be written
But the logarithm of the MULTIPLICITY FUNCTION 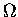 is the definition of the ENTROPY
is the definition of the ENTROPY 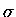 ,
so the
equation can be simplified further to read
,
so the
equation can be simplified further to read
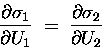 |
(15.9) |
where of course we are assuming that all the other parameters
(like N1 and N2) are held constant.
Note that we have recovered, by strict mathematical methods,
the same criterion dictated by common sense earlier.
The only advantage of the formal derivation is that
it is rigourous, general and involves no questionable
assumptions.15.14


Next: Thermal Equilibrium
Up: Criterion for Equilibrium
Previous: Criterion for Equilibrium
Jess H. Brewer -
Last modified: Mon Nov 16 16:05:37 PST 2015
 - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE ![]() as a function of U1
and
as a function of U1
and ![]() as a function of
U2 = U - U1?
Of course! Why else would I be doing this?
The thing about a maximum of a function
(or a minimum, for that matter; either type of extremum
obeys the same rule) is that the slope of the function
must be zero at the extremum.
[Otherwise it would still have further up or down to go!]
Since the slope is given by the derivative, this reads
as a function of
U2 = U - U1?
Of course! Why else would I be doing this?
The thing about a maximum of a function
(or a minimum, for that matter; either type of extremum
obeys the same rule) is that the slope of the function
must be zero at the extremum.
[Otherwise it would still have further up or down to go!]
Since the slope is given by the derivative, this reads
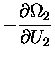 for
for